Through any two points, there exists exactly one line.
Postulate 2 :
A line contains at least two points.
Postulate 3 :
If two lines intersect, then their intersection is exactly one point.
Postulate 4 :
Through any three noncollinear points, there exists exactly one plane.
Postulate 5 :
A plane contains at least three noncollinear points.
Postulate 6 :
If two points lie in a plane, then the line containing them lies in the plane.
Postulate 7 :
If two planes intersect, then their intersection is a line.
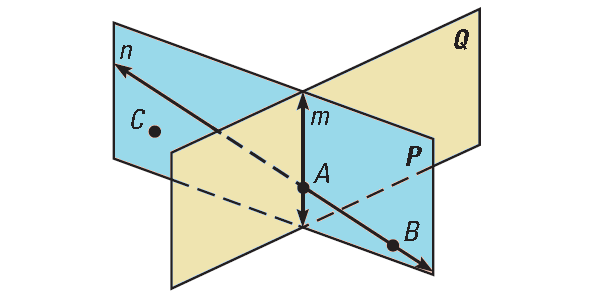
Use the diagram shown below to give examples of postulates 1 through 7.

Postulate 1 :
There is exactly one line (line n) that passes through the points A and B.
Postulate 2 :
Line n contains at least two points. For instance, line n contains the points A and B.
Postulate 3 :
Lines m and n intersect at point A.
Postulate 4 :
Plane P passes through the noncollinear points A, B and C.
Postulate 5 :
Plane P contains at least three noncollinear points A, B and C.
Postulate 6 :
Points A and B lie in plane P. So, line n, which contains points A and B, also lies in plane B.
Postulate 7 :
Planes P and Q intersect. So, they intersect in a line, labeled in the diagram as line m.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com